 by: Frank van den Bovenkamp http://science.trigunamedia.com/geocolor
by: Frank van den Bovenkamp http://science.trigunamedia.com/geocolor
Ask a child the colors of a rainbow or emerging from
a prism, and it will name the primary colors. This is what we call "selective
color empathy": the spectrum of light is not perceived smoothly,
but certain colors seem to stand out for no obvious reason. These are
the colors you first learned as a kid. The fact that other colors are
often named after them, but never the way around, by itself proves they
are special.
Why
are these colors found to be unique? Is there a physical or physiological
basis for such divisions of the visible spectrum, or is it just our
"subjective" perception? In that case, why are the primary
colors always the same, worldwide and throughout history?
Is there a universal, but hidden pattern which guides our conscious
experience?
The
"geometric origin of selective color empathy" is a proof of
such a concept, a new approach which could be called the physics of
conscious experience. It formulates a distinct division of the visible
spectrum accurately accounting for the wavelengths of the primary colors,
and more. As it provides clues for an extended type of underlying wave
physics, it can be a great incentive for further research.
The
primary colors: subjective experience and practical applications
Isaac Newton, when he witnessed how white sunlight was split up in its
composite fractions, was apparently well aware of the fact that actual
color creation only takes place in the brain. Hence, selective perception
of the primary color could essentially be attributed to the brain as
well. Later, physicists discovered the (electro-magnetic) wave nature
of light, and soon enough the wavelengths corresponding to the primary
colors were agreed upon and became establised.
Yet, the selective perception of primary colors as such remained an
entirely subjective phenomenon. The wavelengths, for example like they
are produced by a prism form a smooth gradient, so there seemed little
incentive to even suspect a relevant physical basis for any discrete
division of the visible spectrum.

Nevertheless, there are practical applications which
we all know in daily life. There are different forms of color mixing:
"subtractive" used for printing (i.e. on a white surface),
"additive" e.g. for color tv's or computer monitors (on a
black surface) and artistic mixing. All spectral colors (plus purple)
can thus be created, and by adding black or white also all saturations
and luminosities. If you use a magnifying glass to look at the image
in the centre, you can clearly discern the RGB pixels at work in additive
mixing on your screen in real time!
Allthough this confirms the uniqueness of the primary colors in a practical
sense, it still does not explain a specific physics principle causing
these colors to stand out. They still seem to be just wavelengths like
any other..
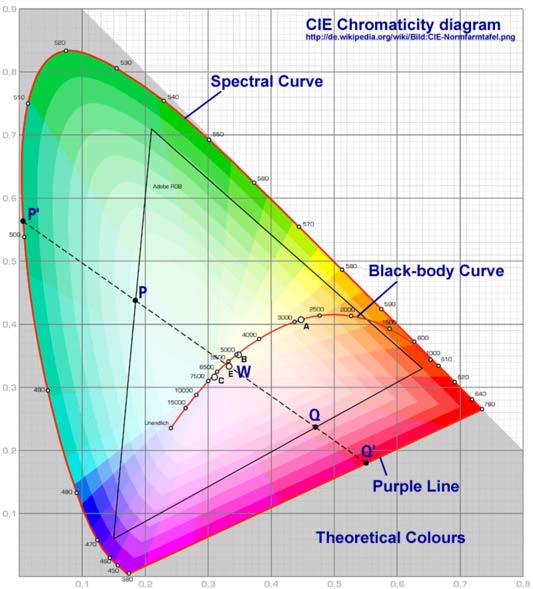
The officially agreed wavelengths of the primary colors
in the so called chromaticity diagram, showing all mixing modes in this
case to create all hues and luminosities.
The
wave matrix physiology of conscious perception: a
possible physical cause of selective color empathy.
Waves
not only have a vibrational quality (frequency), they also have another
aspect, which is their internal momentum. This is very well known in
mathematical physics, but is heavily ignored as it was never considered
to be of practical consequence.
Unlike in physics, for biology (not as a subject but actual organic
life) and life in general this internal momentum of waves is crucially
important.
Now, depending on the type of interaction with other waves, either the
vibrational quality or the inner momentum of a single wave is emphasized.
These "other waves" in that case form a coherent set which
is referred to as a wave matrix in 3 dimensions. A somewhat deeper approach
is, that a coherent wave matrix can represent (or, in a way, produce)
either the vibrational aspect, or the inner momentum of a single wave,
or both.
The specialty is, as currently the actual physics of inner wave momentum
is still little understood and a subject of research, it can alternatively
be referred to indirectly by means of the (normal) frequency
physics of the wave matrix it is part of.
In particular it was found (and can mathematically be proven) that a
wave matrix based on octave ratios between wave lengths, can
equivalently express the vibrational aspect of a single wave.
Likewise, if a wave matrix is based on Golden Mean (Phi-) ratios
it represents the internal momentum of a single wave:
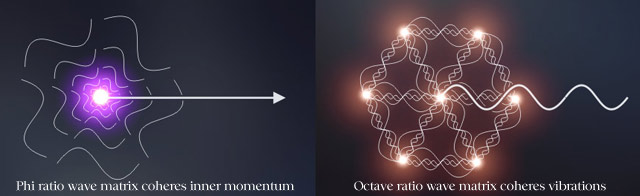
Translated
(approximately) to how the brain functions during perception, this could
be referred to as wave matrix physiology. The deeper understanding
is, that wave matrix physics is the generic cause of conscious perception,
as afterall the brain, and the whole body are themselves but a creation
of that same perception.
In wave matrix physiology, the vibrational aspect of a wave is associated
with the conventional (physics) representation of a wave, as it is captured
by our organic senses. The somewhat mysterious inner momentum is associated
with the actual perception of that wave, roughly speaking, in the brain.
Afterall, we don't literally see or hear waves themselves, but actual
colors or sound.
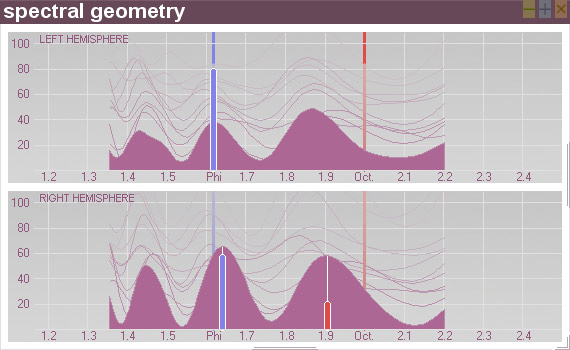
The
NeuroGem
elegantly measures spectral geometry in the EEG and detects
Golden Mean or Octave coherence, while offering a variety of diagnostics
and
training options
Now, the octave resp. Golden Mean wave matrix configurations in 3 dimensions
are conveniently modelled by the regular polyhedrons, that is, the platonic
bodies. The cube (or tetrahedron, used in below animation) represents
the octave wave matrix whereas the dodecahedron represents the Golden
Mean matrix.
It
was then discovered that the allover wave matrix physiology of conscious
perception is represented by the geometric interaction between these
two constellations, called "interdigitation". Below interactive
animations show the basic principle and how this finally results in
the accurate prediction of the primary colors.
3-D
interactive animations showing the geometric origin of selective color
empathy
Drag the grey dot horizontally to control the animation
Note: in order to view the animations, you may
need to "allow blocked contents"
in your browser, depending on th ActiveX security settings. Further
animation
instructions, and browser settings here.
Geometric interdigitation: first an example in 2-D to demonstrate how
co-inciding vertice pairs of two geometric bodies define principal differential
angles, created from the combined geometries. In this 2-D example, not
all vertice pairs are matching at a time (in fact only one) simply because
that would not create interesting new angles.
In real life 3-D, the play of geometric angles is a bit more intricate,
and is now demonstrated to accurately predict the perceived divisions
in the visible spectrum:
Double-click
to start / stop the animation;
drag l-r using right mouse button to set differential angle
Geometric
interdigitation in three dimensions: this is the geometric "machine"
creating the wavelengths of all the primary colors. Like in the 2-D
example, the angle is between the red and blue main axes is determined,
in this case predicting the accurate wavelengths. The donut shaped "photon"
is drawn inside only to directly visualize how the differential angle
(indicated by the blue arrow, as the red one is always zero) indicates
a spectrum color. The auto-rotation takes the animation through the
differential angles, it has no physical meaning.
In terms of real physics, in fact two interacting toroidal topologies
are proposed, interacting at under a certain coupling angle to produce
a net energy corresponding with a specific wavelength. The second torus
is only shown as a circle, to keep the animation simple.
The resulting angle vs. wavelength diagram is shown below:
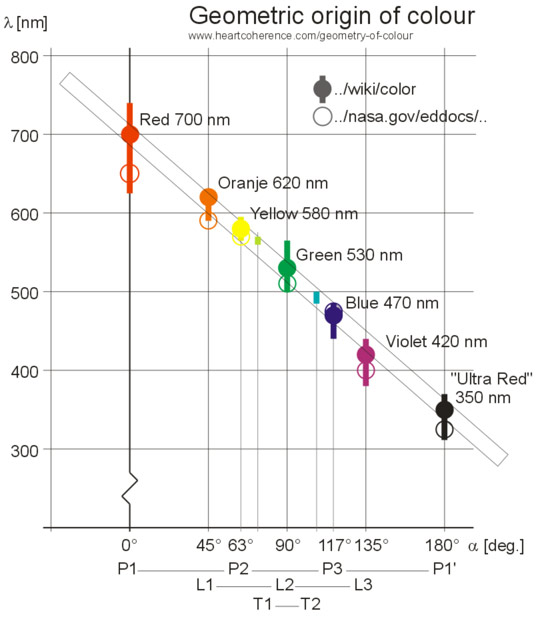
Mapping the geometric angles with the wavelengths of
the primary colors
creates a simple straight line: proof of concept!
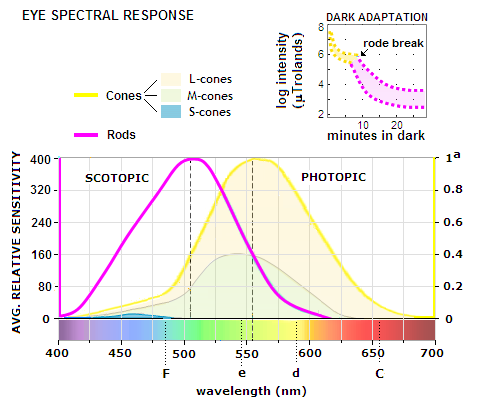
An amazing bonus and further proof: one color designated
by the geometric color formula is generally not perceived to be in any
way specific. But does it? This spectral color, yellowish green, turned
out to accurately match the "photopic"
sensitivity peak of the retina. The official wavelength is 555 nm, the
geometric color formula produced 556 nm - just a fraction of a percent
off the mark!

By way of a rough analogy, it could be said that the series of primary
colors (incl. photopic peak) constitutes the "emission spectrum"
of the wave matrix physiology of conscious perception:
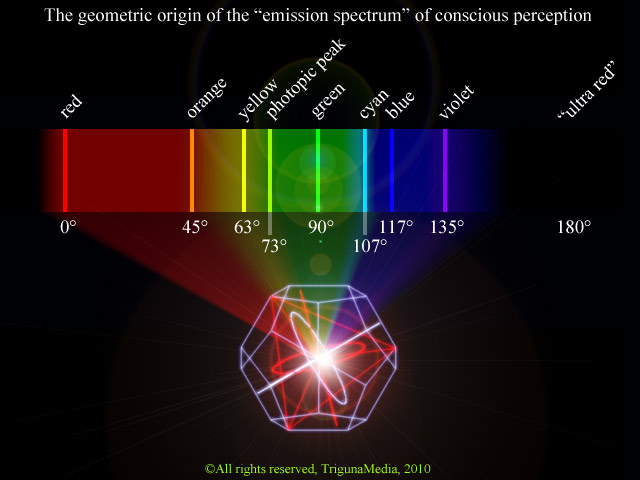
© All rights reserved, TrigunaMedia 2010